The Cost of a Perfect Market Timing Strategy
by P.J. DiNuzzo November 6, 2015
The Cost of a Perfect Market Timing Strategy
What if we could construct a strategy with a correlation close to 1 with a perfect market timing strategy? Can we estimate what its returns would have been? Can we use these estimates to understand what the market would have "charged" for a perfect market timing strategy?
what its returns would have been? Can we use these estimates to understand what the market would have "charged" for a perfect market timing strategy?
To answer these questions, first let's define what a perfect market timing strategy needs to know and what it is. A perfect market timing strategy needs to know, with certainty, the future returns of the assets that are eligible for investment. Armed with this information, the perfect market timing strategy always chooses the highest returning asset to invest in. For example, imagine a strategy that can invest in US stocks [for simplicity, the S&P 500 Total Return (TR) Index] and One-Month US Treasury Bills. It rebalances once per month and on that day knows with certainty the return of US stocks and US Treasury bills over the following month. This perfect market timing strategy would then invest all in equities or all in the One-Month US Treasury Bill, depending on which one will have the higher return over the following month. The challenge here is obvious. How can we know with certainty what the future returns on any asset class will be? Without that knowledge, there is no way to create a perfect market timing strategy. Or is there?
Merton1 (1981) shows how to create a strategy that has an almost perfect correlation with the perfect market timing strategy. In particular, this equity strategy buys one share of stock and a one-month put option with a strike price equal to the current stock price adjusted for the yield on the one-month T-bill. We refer to it as a protected equity strategy. In the absence of costs, the payoffs from the protected equity strategy are identical to the perfect market timing strategy. As shown in the Appendix, the options used in the protected equity strategy are "in-the-money" by the amount of the yield on the T-bill when written at the beginning of each month.
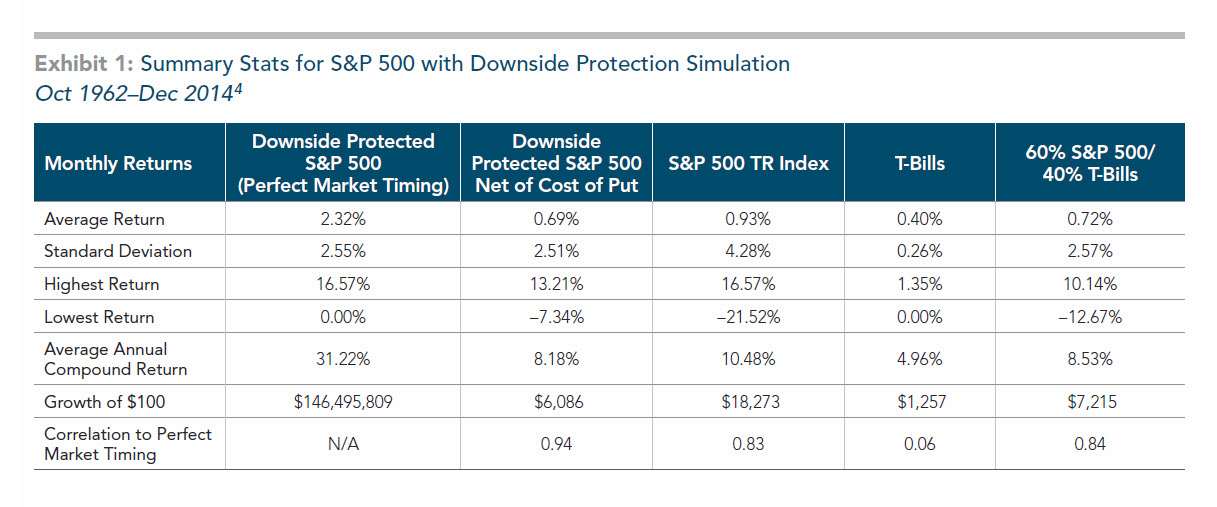
In the absence of costs, the hypothetical returns and wealth generated by the equivalent perfect market timing and protected equity investment strategies are astonishing. For the 1962-2014 sample period, a $100 initial investment grows to over $146 million, much larger than the $18,273 from investing in the S&P 500 Index (see Exhibit 1). But what about the costs associated with the protected equity strategy? Merton argues that the equilibrium market price of the perfect market timing strategy is equal to the cost of the put option required to guarantee at least the T-bill return each month.
Since the put option price can be estimated using the Black-Scholes formula, we could estimate the returns of the protected equity strategy net of the cost of the required put option. The Black-Scholes formula to price stock options requires these inputs: current price of the stock, strike price of the option, risk-less interest rate and expected volatility of the stock's returns over the life of the option. The expected volatility of stock returns is the only input to the Black-Scholes model that must be estimated. In the simulation, we estimate this as the annualized daily volatility of the 60 previous daily returns.2 Exhibit 1 summarizes the results for the 1962-2014 period.
The monthly returns of the perfect market timing and downside protection strategies are highly correlated at 0.94. The minimum monthly return of the perfect market timing strategy was 0.00%. However, the minimum monthly return of the downside protection strategy is -7.34%. This occurred in January 2009 and reflects the cost of purchasing the put option that month. In fact, the estimated average cost of the one-month put option is 1.63% over the sample period. This can be thought of as the market assigned value for perfect market timing. So while the perfect market timing strategy has an average monthly return of 2.32%, the net of cost monthly return of the downside protected equity investment is 0.69% per month, which is smaller than the average monthly return of the S&P 500 Index's 0.93% per month. Hypothetical growth of $100 turns out to be just $6,086 after costs, much less than the value of $100 invested in the S&P 500 Index ($18,273).3
We can now answer our original question: What if we could construct a strategy with a correlation close to 1 with the perfect market timing strategy? It turns out that while this is possible, the cost of implementing would have resulted in inferior performance (in terms of ending wealth) to just holding the S&P 500 Index. If volatility and maximum drawdowns are something an investor is particularly concerned with, a balanced portfolio may be a more cost-effective way to achieve this goal. For example, 60% S&P 500 and 40% T-Bills would have achieved a similar level of volatility to the downside protected strategy with a higher average return-so your $100 would have grown to $7,215.3
Sincerely,

P.J. DiNuzzo, CPA, PFS®, AEP®, AIF®, MSTx, MBA
President, Founder, and Chief Investment Officer
Merton, R. C. 1981. "On Market Timing and Investment Performance. I. An Equilibrium Theory of Value for Market Forecasts." Journal of Business, 1981, Vol. 54, No. 3.
1. Robert Merton provides consulting services to Dimensional Fund Advisors LP.
2. By using actual trailing volatility of 60 previous daily returns, we are following a standard methodology similar to Merton (1981), which uses the volatility of 12 previous monthly returns. However, we note that the market prices of options on average tend to reflect a higher implied level of volatility than the actual realized equity volatility. This would cause our cost estimates to be conservative.
3. Past performance is no guarantee of future results. It is not possible to invest directly in an index.
4. Data Source: S&P 500 Total Return (TR) Index from CRSP Value-Weighted Universe (1962-1988) and S&P 500 TR Index from Bloomberg (1988-2014); One-Month US Treasury Bills from Morningstar. Past performance is not a guarantee of future results. It is not possible to invest directly in an index. Simulated strategy returns based on a model/back-tested simulation. This is not a strategy managed by Dimensional. The performance was achieved with the retroactive application of a model designed with the benefit of hindsight; it does not represent actual investment performance. Back-tested model performance is hypothetical (it does not reflect trading in actual accounts) and is provided for informational purposes only. The securities held in the model may differ significantly from those held in client accounts. Model performance may not reflect the impact that economic and market factors might have had on the advisor's decision making if the advisor were actually managing client money. This strategy was not available for investment in the time periods depicted. Actual management of this type of simulated strategy may result in lower returns than the back-tested results achieved with the benefit of hindsight. Past performance (including hypothetical past performance) does not guarantee future or actual results. The simulated performance shown is "gross performance," which includes the reinvestment of dividends but does not reflect the deduction of investment advisory fees and other expenses.
5. No early exercise, "European" stock options that are relevant for this problem.
About the authors:
Stanley Black, Vice President
Samuel Wang, Researcher



